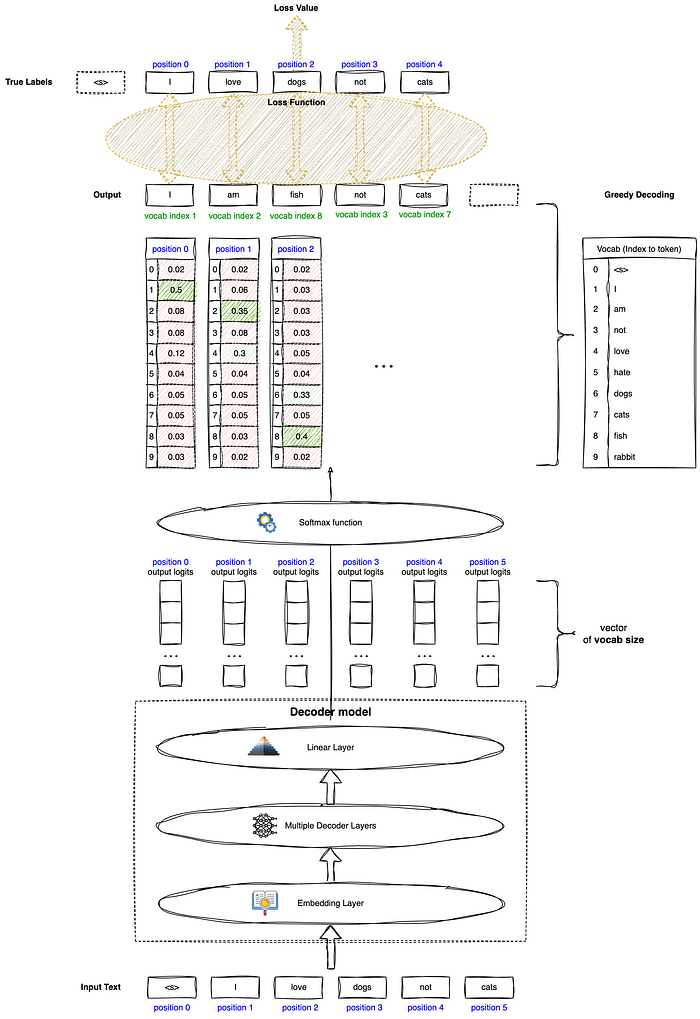
We often read about pre-training Large Language Models (LLMs) but we rarely see a visualisation of how loss is calculated during the training process. This article will attempt to break down and visualise how loss is calculated for a generic LLM. Loss functions determine how the gradient is calculated to update weights during training. Understanding how they are calculated will allow us to understand how the model learns.

First, let's briefly discuss how LLMs generate text and how they are trained!

How do LLMs generate text?

In general terms, shown in Figure 1, LLMs take in a sequence of tokens as input, pass them through its model layers, and output a sequence of logits. Logits would have the size of its vocabulary. Using a Softmax function, we can convert the logits into multiclass probability. "Class" in this case would be tokens or "words" in the model's vocabulary.

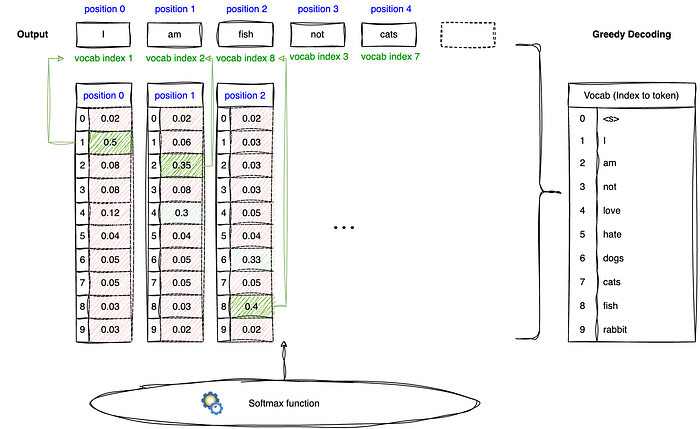
For example, if the model vocabulary has 10 words, we will have a vocab token index of up to 10 as shown in Figure 2's Vocab table. The multiclass probability vector would consist of probabilities corresponding to each of the 10 token indexes as shown. This word probability indicates how likely the model "thinks" the word should be generated at that position. A trivial way of generation would be "greedy decoding" where the token with the highest probability is generated. At position 0, the highest probability would be token 1 which is the word "I" (as mapped from the Vocab table). Position 1 would have the highest probable token of 2 which is the word "am".

How are LLMs pre-trained? What is Causal Language Modeling?

There are many language modeling training techniques (casual and masked) but we will focus on Causal Language Modeling (CLM) in this article. In CLM, the model will be trained to predict the next token or word in a sequence based on preceding tokens. This is normally used to train text generative models like GPT. The predicted "next token" will then be compared with the true token during training. Thus, during CLM, True labels are taken as the input tokens shifted to the left by 1 position.

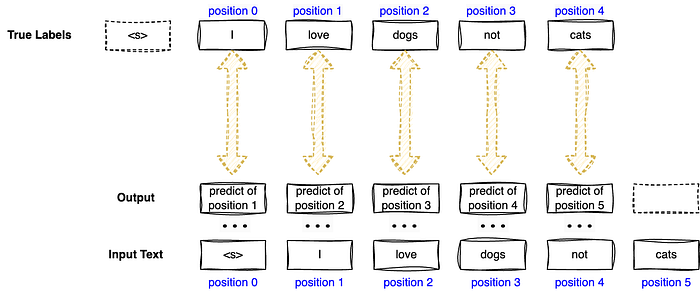
For example, if our input text is "<s> I love dogs not cats", our true labels will be "I love dogs not cats" which are shifted from the input. As shown in Figure 3, input at position 2 is "love", consequently, output at position 2 will be a prediction of position 3 which is the word "dogs". Thus, the true label at position 2 will be taken as "dogs" and we will compare the output at position 2 with the token "dogs". Loss is calculated from this comparison of output and true labels. The model will then learn from this loss. Essentially, we are measuring the model's ability to predict the next word.

Loss Visualisation!

Let's see how the loss value is calculated. There are many loss functions available but we will discuss the Cross Entropy Loss in this article. As seen in Figure 1, the softmax function will output a multiclass probability vector for each position of the sequence. This probability vector will be used in the calculation of the loss in the following way.

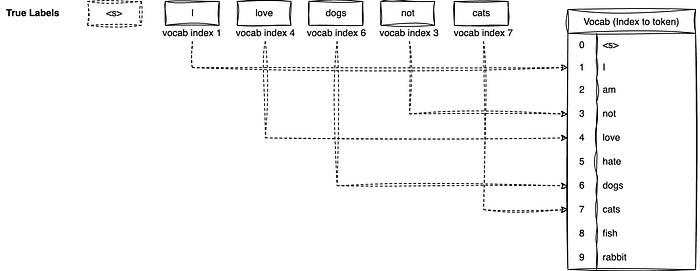
Step 1: The vocab token index of true labels will have to be extracted. As shown in Figure 4, referencing the Vocab table, the true label at position 0 "I" would have an index of 1. True label at position 1 "love" would have an index of 4.

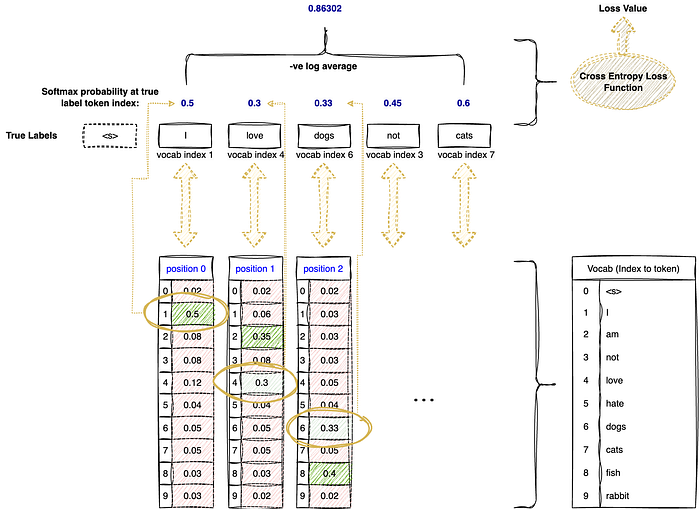
Step 2: Probability at the true label's vocab token index will be taken. The probability taken at position 0 would be 0.5, position 1 would be 0.3, and so on. This can be seen from the multiclass probability vector examples for positions 0, 1 & 2 in Figure 5.

Step 3: Once we have the softmax probabilities, we will apply a negative log and aggregate them by taking the mean. From the example in Figure 2, our Cross Entropy loss will be mean([-log(0.5), -log(0.3),-log(0.33),-log(0.45),-log(0.6)]) = 0.86302.

In other words, cross-entropy loss is measuring if the model gives the true "next word" a high probability. The lower the loss, the higher the model probability of the true "next word". The model learns to better generate the "next word" during training by updating its weights to lower the loss.

How it looks like in code!

import transformers
from transformers import AutoModelForCausalLM, AutoTokenizer
import torch
from torch.nn import CrossEntropyLoss

# personal huggingface access token will be needed to use Llama2 models
ACCESS_TOKEN_WRITE = # hugging face access token
cache_dir_local = # dir for cache

BASE_MODEL = "meta-llama/Llama-2-7b-hf"

# initialise tokenizer
llama2_tokenizer = \
AutoTokenizer.\
from_pretrained(BASE_MODEL, 
                padding_side="left", 
                use_auth_token=ACCESS_TOKEN_WRITE,
               cache_dir=cache_dir_local)

# initialise model
llama2_model = \
AutoModelForCausalLM.from_pretrained(
    BASE_MODEL, 
    use_cache=True,
    device_map="auto",
    cache_dir=cache_dir_local,
    use_auth_token=ACCESS_TOKEN_WRITE)

# example input text
text_input = 'I love dogs not cats'
toks = llama2_tokenizer(text_input, return_tensors='pt')
# labels of CLM can be taken as inputs, huggingface will handle the shifting of the labels as mentioned above.
toks['labels'] = toks['input_ids']

out = llama2_model(**toks, output_hidden_states=True, return_dict=True)
print(out['loss'])
# tensor(4.6854, grad_fn=<NllLossBackward0>)

We use Llama 2 as the LLM model. The default loss function from the huggingface wrapper is Cross Entropy as well and we can see that the loss calculated is 4.6854. Now let's try to calculate the loss manually.

logits = out['logits']
labels = toks['labels']
# following model wrapper in huggingface
shift_logits = logits[..., :-1, :].contiguous()
shift_labels = labels[..., 1:].contiguous()
# flatten batch
shift_logits = shift_logits.view(-1, 32000)
shift_labels = shift_labels.view(-1)

print(shift_labels)
# tensor([  306,  5360, 26361,   451,   274,  1446])

First, we extract the token indexes of the true labels [ 306, 5360, 26361, 451, 274, 1446].

softmax_prob_at_label_tokidx = \
torch.nn.Softmax()(shift_logits)[torch.arange(shift_labels.size(-1)), shift_labels]
print(softmax_prob_at_label_tokidx)
# tensor([1.0475e-02, 1.5564e-02, 8.7919e-04, 1.5152e-04, 2.8680e-02, 9.9225e-01],
# grad_fn=<IndexBackward0>)

Next, we apply the softmax function to the output logits and take the probability at the true label token index as shown in the comments.

loss = (softmax_prob_at_label_tokidx.log() * -1).mean()
print(loss)
# tensor(4.6854, grad_fn=<MeanBackward0>)

# double checking with cross entropy function
print(CrossEntropyLoss()(shift_logits, shift_labels))
# tensor(4.6854, grad_fn=<NllLossBackward0>)

Finally, we apply the negative log and mean aggregation and see that the loss calculated manually is also 4.6854.